2022.02.10

　今回は、前回の「累乗」の話の続きとして、「ハノイの塔」というパズルについて、語っていこうと思います。

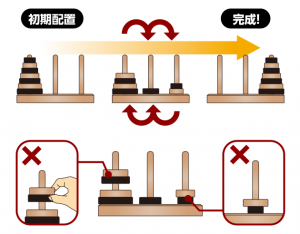
ハノイの塔とは、左の写真のような３つの杭に穴が開いた大きさの違う円盤が刺さってピラミッド状になっているものを、あるルールに沿って動かして、別の杭にピラミッドを移動させるパズルです。

動かす際のルールは、次の通りです。

「円盤を一回に一枚ずつどれかの杭に移動させることができるが、小さな円盤の上に大きな円盤を乗せることはできない」

実は、このハノイの塔には、ちょっとした伝説があり、詳しい話は省きますが、「円盤が６４枚ある状態のハノイの塔で、先ほどのルールに沿って、別の場所に塔を完成させると世界は消滅してしまう」という話があります。

ちょっと何を言っているかわからないかもしれませんが、６４枚の円盤を動かして塔を別の場所へ完成させるころには、地球は本当になくなっているかもしれません。

　実際にハノイの塔を動かすのに、どれくらい移動させればいいのかを検証してみると次のようなことが分かります。

円盤６４枚をすべて、別の場所へ移動させるために必要な移動回数は、

「２×２×２×…×２×２（２を６４回かけて）－１」の回数となります。

前回行った累乗計算がありますね。累乗の増え方は前回お伝えした通りなので、実際にどれくらいの回数と時間がかかるのかを計算してみました。

仮に、１枚の円盤を動かすのに１秒かかるとして計算すると…

１８００京（秒）かかります。※「京」は億のうえの兆のさらに上の数です。

年に換算すると「約５８００億年」となります。

太陽の寿命が、約５０億年といわれていて、その最後の時には爆発する太陽に地球は飲み込まれてしまうともいわれているため、せいぜい長くても地球の寿命は５０億年といったところでしょう。

それを考えれば、本当にハノイの塔が完成するころには、地球は消滅していそうですね。